Unicité du point fixe donnée par inégalité de contraction.

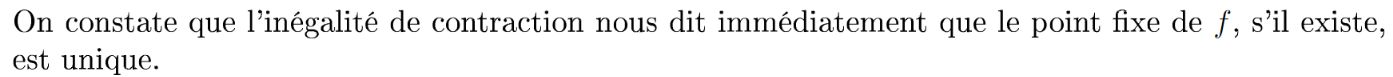
Montrer que la suite récurrente est de Cauchy en utilisant la contraction de \(f\).

On a donc la convergence par complétude de \(E\).
La suite est donc de Cauchy, et donc converge dans \(E\) complet.

Par passage à la limite dans \(x_{n+1}=f(x_n)\), on en déduit que la limite \(x\) est point fixe de \(f\).

On fait tendre \(p\to+\infty\) dans l'inégalité précédente pour obtenir la vitesse de convergence.

On pose \(A\), qui associe à une fonction la fonction donnée par l'énoncé.

On peut la majorer via la norme uniforme et trouver qu'elle est contractante.

Trouver une solution sur \([0,\frac12]\) via le théorème du point fixe de Banach-Picard.

Etendre à tout \([1/2,1]\) en ajoutant une constante.

On est dans un Banach, et une composante est lipschitzienne.

On montre que \(A\) est contractante

On conclut en utilisant le théorème du point fixe de Banach-Picard.